Ideal Info About What Is The Difference Between Continuity And Discontinuity

Unraveling Continuity and Discontinuity

1. What Exactly Are We Talking About?

Ever wondered what mathematicians mean when they throw around words like "continuity" and "discontinuity"? Don't worry, it's not as scary as it sounds! Imagine drawing a line on a piece of paper without lifting your pen. That's continuity in action. Now, imagine you have to lift your pen to continue the line. That's discontinuity barging in and messing things up! Think of it like a smoothly paved road versus one with a giant pothole. Which one would you rather drive on?

In the world of math, specifically calculus, continuity refers to a function whose graph can be drawn without lifting your pen. A discontinuous function, on the other hand, has breaks, jumps, or holes in its graph. These "breaks" are where the function isn't, well, behaving continuously. It's all about whether the function smoothly flows from one point to the next.

So, the main difference boils down to this: Can you trace the graph without lifting your pen? If yes, it's continuous. If no, it's discontinuous. This seemingly simple concept has profound implications in many areas of mathematics and physics. For instance, continuous functions are often easier to work with when solving equations or modeling real-world phenomena. Discontinuous functions, while trickier, are essential for describing situations that involve sudden changes or jumps, such as the switching of a light or the sudden impact of a ball.

In layman's terms, continuity represents a smooth transition, while discontinuity represents an abrupt change. Understanding this fundamental difference is crucial for grasping more advanced mathematical concepts and their applications in various fields. Think of it as the difference between a gentle slope and a sheer cliff both are part of the landscape, but they certainly require different approaches!

Digging Deeper

2. Not All Breaks Are Created Equal

Now that we know what discontinuity is, let's explore the different flavors it comes in. There are a few main types, each with its own unique characteristics and quirks. Understanding these types can help you better analyze and work with discontinuous functions.

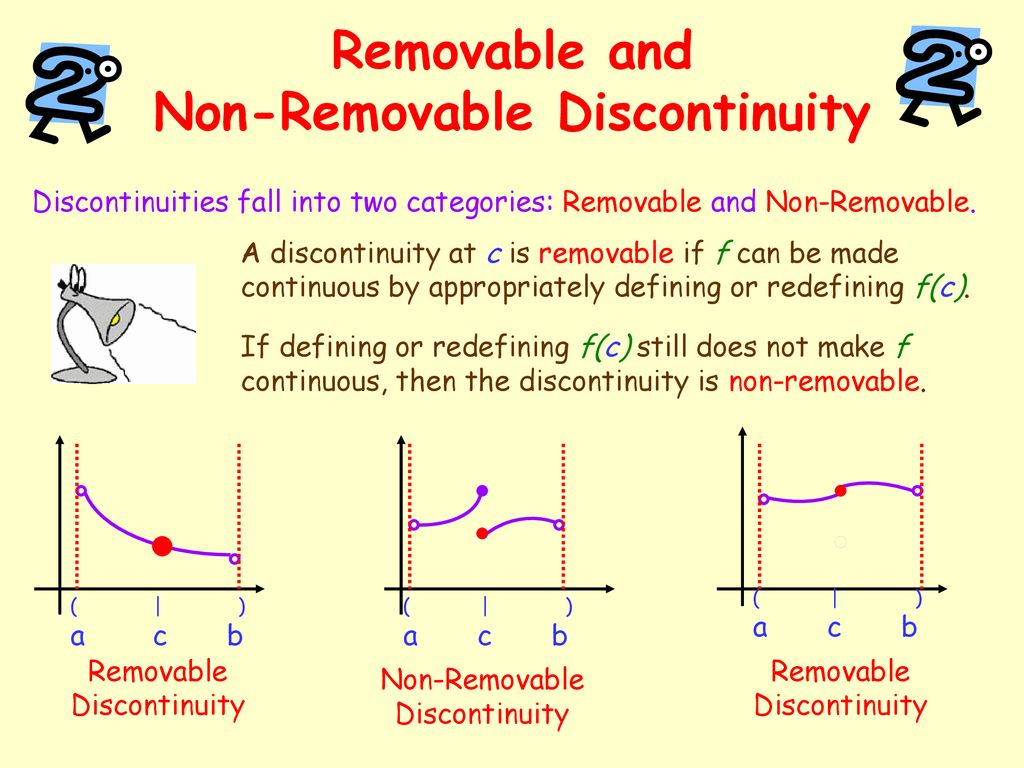
First, we have removable discontinuities. These are like little hiccups in the function's graph. There's a hole at a specific point, but if you "filled it in" by redefining the function at that point, it would become continuous. Think of it like a missing puzzle piece that, once placed, completes the picture. These are often caused by factors that cancel out in the function's equation, leaving a lone point undefined.

Next, there are jump discontinuities. These are more dramatic. The function "jumps" from one value to another at a specific point. Imagine climbing a staircase — you step up from one level to the next. You can't smoothly transition between them. Jump discontinuities occur when the left-hand limit and the right-hand limit at a point exist but are not equal.

Finally, we have infinite discontinuities. These occur when the function approaches infinity (or negative infinity) as it gets closer to a certain point. Think of a vertical asymptote on a graph. The function shoots off towards infinity, never actually reaching the line. These are often found in rational functions where the denominator approaches zero.

Why Does Continuity (and Discontinuity) Matter?

3. Real-World Applications and Implications

Okay, so we know what continuity and discontinuity are. But why should you care? Well, they're not just abstract mathematical concepts. They show up in surprising places in the real world!

Consider the design of a bridge. Engineers need to ensure that the bridge's structure is continuous to avoid any sudden breaks or weaknesses. They use continuous functions to model the stress and strain on the bridge under various conditions. A discontinuity could represent a critical point where the bridge is more vulnerable to failure. This is an area where mistakes simply aren't acceptable.

In computer graphics, continuity is essential for creating smooth and realistic animations. Think about a character moving across the screen. If the motion isn't continuous, it will appear jerky and unnatural. Computer programmers utilize continuous functions to define the character's trajectory, ensuring that it moves seamlessly from one position to the next. Discontinuities can manifest as sudden glitches or jumps in the animation.

Even in economics, the concept of continuity plays a role. Economists might use continuous functions to model the supply and demand of a product. While real-world economic scenarios are often messy and complex, the assumption of continuity can help simplify the analysis and make predictions. A discontinuity could represent a sudden shift in market conditions, such as a major policy change or a natural disaster. Therefore, knowing these facts are essential to understanding how the market operates.

In simple terms, continuity allows us to build stable structures, create smooth animations, and make reasonable predictions. Discontinuity signals points where things might break, change suddenly, or become unpredictable. Recognizing the difference is important for navigating the world around us.

How to Determine Continuity

4. Tests and Techniques

So, how do you actually determine if a function is continuous at a specific point? Luckily, there are a few straightforward tests you can use. It's like being a detective, searching for clues that reveal the function's true nature.

First, the function must be defined at that point. In other words, if you plug the point into the function, you should get a real number. If the function is undefined (e.g., division by zero), it's definitely discontinuous at that point. This is the most basic requirement for continuity and is often overlooked.

Second, the limit of the function as it approaches the point must exist. This means that the function should approach the same value from both the left and the right. If the left-hand limit and the right-hand limit are different, the function has a jump discontinuity at that point. Evaluating the limit is often the most challenging step, but it's crucial for determining continuity.

Third, the value of the function at the point must be equal to the limit of the function as it approaches the point. If these two values are different, the function has a removable discontinuity. This condition ensures that there's no "hole" in the graph at that point.

If all three of these conditions are met, then the function is continuous at that point. If any of these conditions fail, the function is discontinuous. By systematically applying these tests, you can confidently determine the continuity of a function at any given point.

Continuity and Discontinuity

5. Advanced Considerations

While the basic concepts of continuity and discontinuity are relatively straightforward, things can get a bit more complex when you delve into more advanced topics. Let's explore some of these nuances and considerations.

For instance, we can talk about continuity on an interval, not just at a single point. A function is continuous on an interval if it's continuous at every point within that interval. This is important for analyzing the overall behavior of a function over a range of values. Consider a continuous function on a closed interval; such functions possess special properties, like the extreme value theorem, guaranteeing that the function attains a maximum and a minimum value within that interval.

Another important concept is uniform continuity. This is a stronger form of continuity that requires the function to be "equally continuous" across the entire domain. In simpler terms, for any given level of closeness in the output, you can find a corresponding level of closeness in the input that works everywhere. Uniform continuity is crucial for proving the convergence of certain numerical methods and for establishing the existence and uniqueness of solutions to differential equations.

Finally, the study of discontinuous functions is a rich and fascinating area of mathematics. Discontinuities can be used to model a wide variety of real-world phenomena, from the breaking of a dam to the firing of a neuron. Understanding the properties of discontinuous functions is essential for solving problems in physics, engineering, and other fields. While challenging, discontinuous functions provide powerful tools for analyzing situations involving sudden changes or jumps.

Furthermore, it's vital to understand that continuity and discontinuity are relative to the domain of the function. A function that is discontinuous when considered across all real numbers may be continuous when its domain is restricted to a specific interval. This highlights the importance of carefully defining the domain when analyzing the continuity of a function.

FAQ

6. Let's Clear Up Any Confusion

Still scratching your head? Here are some common questions people have about continuity and discontinuity.

Q: Can a function be both continuous and discontinuous?
A: Not at the same point! A function is either continuous or discontinuous at a specific point. However, a function can be continuous over some intervals and discontinuous over others. Think of a road that has some smooth stretches and some parts with potholes.

Q: Is a vertical line continuous?
A: Not as a function. Vertical lines cannot be represented as functions of x because they fail the vertical line test (a single x-value corresponds to multiple y-values). However, lines in general are considered continuous in terms of geometry.

Q: Why does anyone care about continuity? It sounds so theoretical.
A: It's not just theoretical! Continuity underlies many real-world applications, from engineering to computer graphics to economics. It allows us to build stable structures, create smooth animations, and make reasonable predictions. In essence, it's the foundation for many mathematical models we use to understand the world around us.

Q: What's the easiest way to spot a discontinuity?
A: Look for breaks, jumps, or holes in the graph of the function. If you can't draw the graph without lifting your pen, you've got a discontinuity! Alternatively, check for division by zero, square roots of negative numbers (if dealing with real-valued functions), or other potential undefined values.